I°) Définition
Deux points A et A' sont symétriques par rapport à une droite (D) signifie que (D) est la médiatrice du segment [AA'].
|
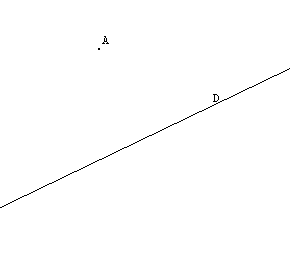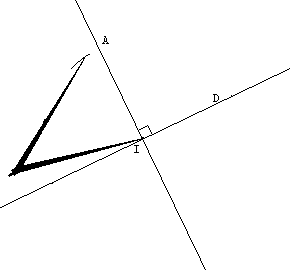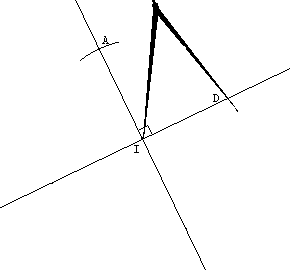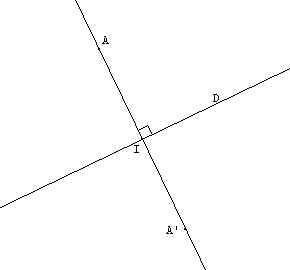
Construction à la règle,
à l'équerre et au compas.
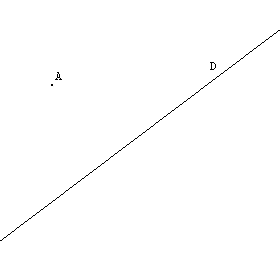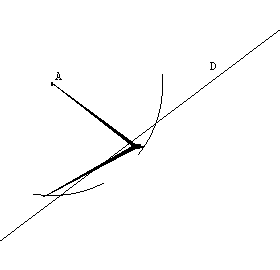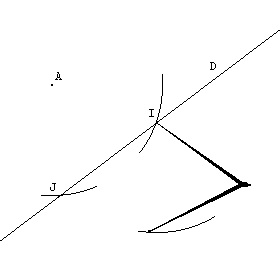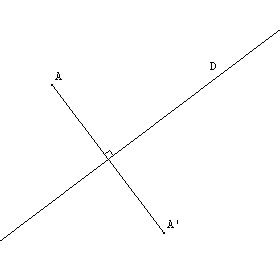
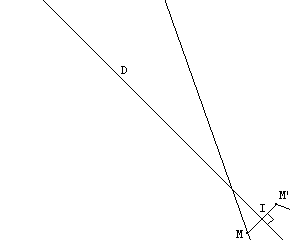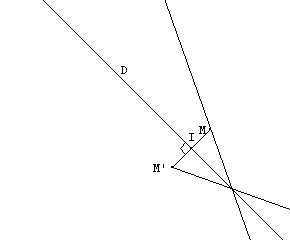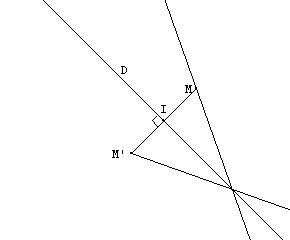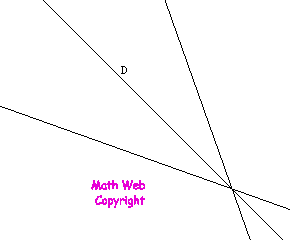
On abaisse de A la perpendiculaire à la droite (D). Soit I le pied de cette perpendiculaire. On place au compas A' tel que IA = IA'. (AA') _|_ (D) et IA = IA' |
II°) Autre construction
| On trace un cercle C de centre
A coupant la droite D en deux points I et J.
On trace alors deux arcs de cercle de centre I et J , de même rayon. Ces deux arcs se coupent en A'. Le point A' est donc le symétrique de A par rapport à D. |
|
|
L'image d'une droite dans la
symétrie autour de (D) est une droite
En général ces droites sont sécantes sur (D). |
| L'image d'un cercle dans la
symétrie autour de (D) est un cercle.
I' est l'image de I, les deux cercles ont le même rayon. |
|
|
){kind=link}
){kind=link}
){kind=link}
){kind=link}