THE RHOMBUS
THE RHOMBUS
I°) Definition
| A rhombus is a quadrilateral whose four sides are of equal length. | ||
|
Let A and B be two points in a plan. Place a point D on the circle of center A and radius AB. It was therefore AB = AD. |
||
Replay animation |
Draw circles of center B and D of radius AB. C is called the point of intersection other than A. |
|
|
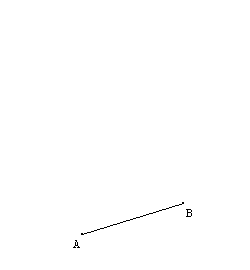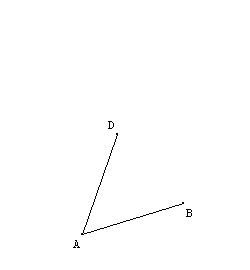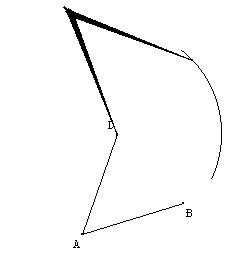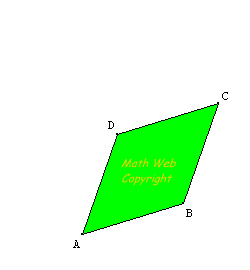
It has AB = BC = CD = DA. quadrilateral ABCD is a rhombus. |
||
II°) 1st property : Characteristic of diamond.
| A rhombus is a parallelogram with two consecutive sides of the same length.
Conversely, a parallelogram with two consecutive sides of the same length is a diamond. Exemple: ABCD est un parallélogramme. Si AB=AD, alors ABCD est un losange. |
Replay animation |
Les diamond thus have the properties of parallelograms.
III°) 2nd property: Characteristic of diamond.
| A rhombus is a parallelogram whose diagonals are perpendicular.
Conversely, a parallelogram with perpendicular diagonals is a rhombus. Example: ABCD is a parallelogram. If (AB) and (AD) are perpendicular, then ABCD is a rhombus. |
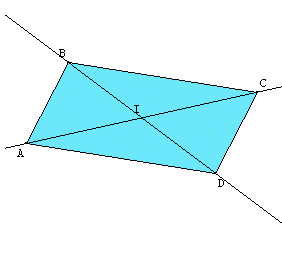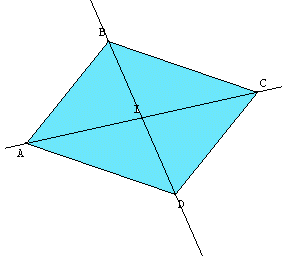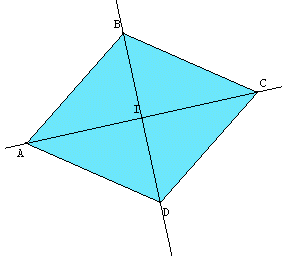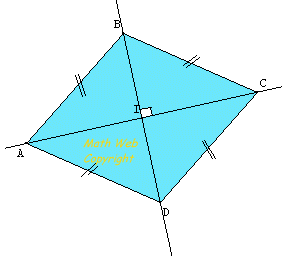
Replay animation |
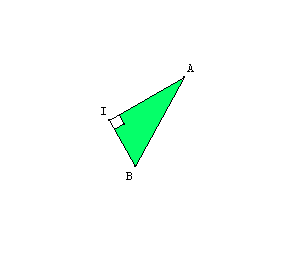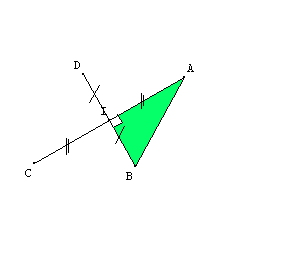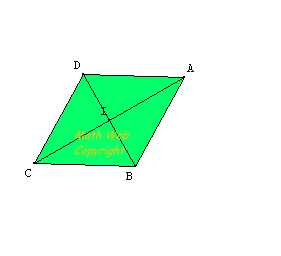
IV°) Axes and centers of symmetry of a rhombus.
| In a rhombus:
- the diagonals are lines of symmetry - the intersection of the diagonals is the center of symmetry |
Replay animation |
|
){kind=link}
){kind=link}
){kind=link}
){kind=link}